Question

Help with this question.....​

Answer 1

`g_(moon)=1.67 [m/s^(2) ]`

Step-by-step explanation:

The weight of some mass is defined as the product of mass by gravitational acceleration. In this way using the following formula we can find the weight.

`w =m*g\\`

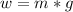
where:

w = weight [N]

m = mass = 0.06 [kg]

g = gravity acceleration = 10 [N/kg]

Therefore:

`w=0.06*10\\w=0.6[N]`

By Hooke's law we know that the force in a spring can be calculated by means of the following expression.

`F=W\\F = k*x`

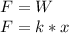
where:

k = spring constant [N/m]

x = deformed distance = 6 [cm] = 0.06 [m]

We can find the spring constant.

`k= F/x\\k=0.6/0.06\\k=10 [N/m]`

Since we use the same spring on the moon and the same mass, the constant of the spring does not change, the same goes for the mass.

`F_(moon)=k*0.01\\F = 10*0.01\\F=0.1[N]`

Since this force is equal to the weight, we can now determine the gravitational acceleration.

`F=m*g_(moon)\\g=F/m\\g = 0.1/0.06\\g_(moon) = 1.67[m/s^(2) ]`