Question

A chunk of glass of density 2500 kg/m3 is suspended from a string and submerged in water. At equilibrium, the buoyant force on the glass from the surrounding water is 50 Newtons. What is the tension in the string?

Answer 1

T=75N

Step-by-step explanation:

In order to solve this problem, we must first start by drawing a free body diagram (see attached picture).

Once we got the free body diagram, we can do an addition of forces so we get:

`\sum F=0`

it equals zero because it's at equilibrium.

So the sum of forces in this case will be:

`T+F_(b)-W=0`

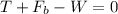
so now we solve for the tension T:

`T=W-F_(b)`

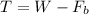
we need to figure out what W is equal to. But in order to do that, we need to figure out what the volume of the glass is. We know the buoyant force is calculated by multiplying the volume displaces by the density of water and the acceleration of gravity, so we get:

`F_(b)=V\rho_(H2O)g`

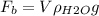
So the volume of the glass will be:

`V=(F_(b))/(\rho_(H2O)g)`

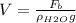
we know the density of water is
`1000 kg/m^(3)`

so our volume is:

`V=(50N)/((1000 kg/m^(3))(9.81 m/s^(2)))`

`V=5.097x10^(-3) m^(3)`

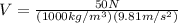
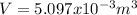
Now we can calculate the weght of the piece of glass, so we get:

`W=\rho_(glass)gV`

`W=(2500 kg/m^(3))(9.81 m/s^(2))(5.097x10^(-3)`

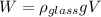
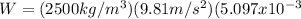
W=125N

and now we can calculate the tension:

`T=W-F_(b)`

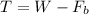
T=125N-50N

T=75N