Answer:
A. The length of the third side is approximately 5 feet.
B. A =
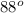 , B =
, B =
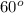 and C =
and C =
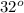 .
.
Explanation:
Let the triangle be ABC. Given two sides and an included angle, let us apply the cosine rule to determine the third length.
A. Let side a = 6 feet and c = 3 feet, thus;
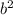 =
=
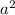 +
+
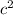 - 2ac Cos B
- 2ac Cos B
=
 +
+
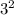 - 2(6 x 3) Cos
- 2(6 x 3) Cos
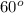
= 36 + 9 - 36 x 0.5
= 45 - 18
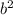 = 27
= 27
b =
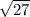
= 5.1962
b = 5.2 feet
b ≅ 5 feet
The length of the third side is approximately 5 feet.
B. Given that B =
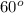 , then let us apply the Sine rule to determined the measure of A.
, then let us apply the Sine rule to determined the measure of A.
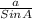 =
=
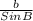
So that,
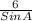 =
=
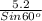
Sin A =
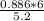
Sin A = 0.99923
A =
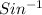 0.99923
0.99923
= 87.75
A ≅
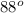
Since the sum of angle in a triangle =
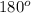 .
.
Then,
A + B + C =
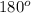
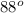 +
+
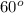 + C =
+ C =
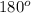
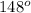 + C =
+ C =
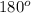
C =
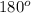 -
-
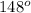
=
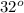
C =
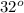
Thus,
A =
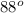 , B =
, B =
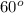 and C =
and C =
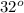 .
.