Question

The radius r of a sphere is increasing at a constant rate of 0.04 centimeters per second. (Note: The volume of a sphere with radius r is V=4/3 pi r³.)

At the time when the radius of the sphere is 10 centimeters, what is the rate of increase of its volume?
​

Answer 1

The rate of the volume increase will be
`(dV)/(dt)=50.27 cm^(3)/s`

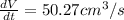
Explanation:

Let's take the derivative with respect to time on each side of the volume equation.

`(dV)/(dt)=4\pi R^(2)(dR)/(dt)`

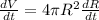
Now, we just need to put all the values on the rate equation.

We know that:

dR/dt is 0.04 cm/s

And we need to know what is dV/dt when R = 10 cm.

Therefore using the equation of the volume rate:

`(dV)/(dt)=4\pi 10^(2)0.04`

`(dV)/(dt)=50.27 cm^(3)/s`

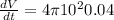
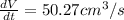
I hope it helps you!