Question

Please help me! Due soon!

The quadratic
`3x^2+4x-9` has two real roots. What is the sum of the squares of these roots? Express your answer as a common fraction in lowest terms.

Answer 1

70/9

Explanation:

We have the quadratic:

`3x^2+4x-9`

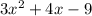
So, let’s find the roots of the quadratic. We will set the expression equal to 0:

`3x^2+4x-9=0`

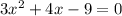
Testing for factors, we can see that our quadratic isn’t factorable.

So, we can use the Quadratic Formula. The quadratic formula is given by:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

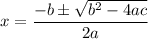
In this case:

`a=3, b=4,\text{ and } c=-9`

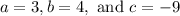
Therefore, by substitution:

`\displaystyle x=(-(4)\pm√((4)^2-4(3)(-9)))/(2(3))`

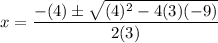
Evaluate:

`\displaystyle x=(-4\pm√(124))/(6)`

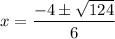
Simplify the square root:

`√(124)=√(4\cdot31)=2√(31)`

Hence:

`\displaystyle x=(-4\pm2√(31))/(6)`

Reduce:

`\displaystyle x=(-2\pm√(31))/(3)`

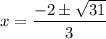
So, our roots are:

`\displaystyle x_1=(-2+√(31))/(3), x_2=(-2-√(31))/(3)`

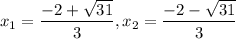
We want to find the sum of the squares of our two roots. So, let’s square each term:

`\displaystyle (x_1)^2=\Big((-2+√(31))/(3)\Big)^2`

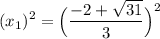
Square. For the numerator, we can use the perfect square trinomial patten where:

`(a+b)^2=(a^2+2ab+b^2)`

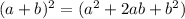
Therefore:

`\displaystyle (x_1)^2=\Big(((-2)^2+2(-2)(√(31))+(√(31))^2)/(9)\Big)`

Simplify:

`\displaystyle (x_1)^2=(35-4√(31))/(9)`

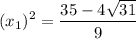
Similarly, for the second root, we will have:

`\displaystyle (x_2)^2=\Big((-2-√(31))/(3)\Big)^2`

So:

`\displaystyle (x_2)^2=\Big(((-2)^2+2(-2)(-√(31))+(-√(31))^2)/(9)\Big)`

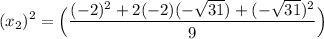
Simplify:

`\displaystyle (x_2)^2=(35+4√(31))/(9)`

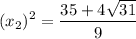
Therefore, our sum will be:

`\displaystyle (x_1)^2+(x_2)^2\\\\ \begin{aligned} &=(35-4√(31))/(9)+(35+4√(31))/(9)\\&=(35-4√(31)+35+4√(31))/(9)\\&=(70)/(9)\end{aligned}`

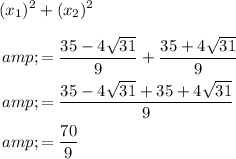
Therefore, our final answer is 70/9.