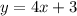Question

Write an equation of the line below

Answer 1

The equation of the line is:

`y = 4x + 3`

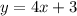
Explanation:

We know that the slope-intercept of line equation is

`y = mx+b`

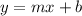
Where m is the slope and b is the y-intercept

Given the two points on a line

• (0, 3)

• (-2, -5)

Finding the slope between (0, 3) and (-2, -5)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(0,\:3\right),\:\left(x_2,\:y_2\right)=\left(-2,\:-5\right)`

`m=(-5-3)/(-2-0)`

`m=4`

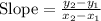
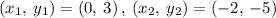
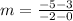
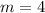
We know that the y-intercept can be computed by setting x=0 and determining the corresponding y-value.

From the graph, it is clear:

at x = 0, y = 3

Thus, y-intercept = b = 3

Substituting m = 4 and b = 3 in the slope-intercept form of line equation

`y = mx+b`

`y = 4x + 3`

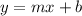
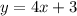
Therefore, the equation of the line is:

`y = 4x + 3`