Question

a car traveling at 28.4 m/s undergoes a constant deceleration of 1.92 m/s2 when the breaks are applied. How many revolutions does each tire make before the car comes to a stop

Answer 1

Complete Question

a car traveling at 28.4 m/s undergoes a constant deceleration of 1.92 m/s2 when the breaks are applied. How many revolutions does each tire make before the car comes to a stop? Assume that the car does not skid and that each tire has a radius of 0.307 m. Answer in units of rev.

Answer:

The value is
`N = 109 \ rev`

Step-by-step explanation:

From the question we are told that

The speed of the car is
`u = 28.4 \ m/s`

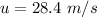
The constant deceleration experienced is
`a = 1.92 \ m/s^2`

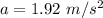
The radius of the tire is
`r = 0.307 \ m`

Generally from kinematic equation we have that

`v^2 = u^2 + 2as`

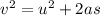
Here v is the final velocity which is 0 m/s

So

`0^2 = 28.4^2 + 2 * 1.92 * s`

=>
`s = 210.04 \ m`

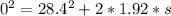
Generally the circumference of the tire is mathematically represented as

`C = 2 \pi r`

=>
`C = 2 * 3.142 * 0.307`

=>
`C = 1.929 \ m`

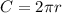
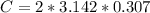
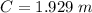
Generally the number of revolution is mathematically represented as

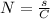
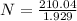
`N = ( s)/(C)`

=>
`N = (210.04)/(1.929)`

=>
`N = 109 \ rev`