Question

A ball is thrown vertically upward with a

speed of 27.9 m/s.
How high does it rise? The acceleration due
to gravity is 9.8 m/s
2
.
Answer in units of m.
008 (part 2 of 4) 10.0 points
How long does it take to reach its highest
point?
Answer in units of s.

Answer 1

1) The maximum height reached is approximately 39.715 m

2) The time it takes the ball to reach the its highest point is approximately 2.85 s

Step-by-step explanation:

1) The vertical velocity of the ball, u = 27.9 m/s

The acceleration due gravity, g = 9.8 m/s²

The kinematic equation that gives the height, h, reached by the ball is given as follows;

v² = u² - 2·g·h

Where;

v = The final velocity of the ball = 0 m/s at the maximum height

h = The height reached by the ball =
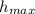`h_(max)` at maximum height

Therefore, by substitution of the known values, we have;

v² = u² - 2·g·h

0² = 27.9² - 2 × 9.8 ×
`h_(max)`

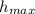
2 × 9.8 ×
`h_(max)` = 27.9²

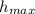`h_(max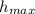)` = 27.9²/(2×9.8) ≈ 39.715

The maximum height reached =
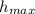`h_(max)` ≈ 39.715 m

2) From the kinematic equation of motion, v = u - g·t, we have the time, t, it takes the ball to reach the maximum height given as follows

At maximum height, the final velocity, v = 0 m/s, therefore, we have;

0 = 27.9 - 9.8 × t

9.8 × t = 27.9

t = 27.9/9.8 ≈ 2.85

The time it takes the ball to reach the maximum height = t ≈ 2.85 seconds.