Question

The half-life of phosphorus-32 is approximately 24.3 days.

Determine a so that A(t)=A0at describes the amount of phosphorus-32 left after t days, where A0 is the amount at time t=0. ROUND TO SIX DECIMAL PLACES.

Please help every answer has been incorrect so far.

Answer 1

`A=A_0(0.971878)^t`

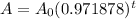
Explanation:

The half-life of Phosphorus-32 is approximately 24.3 days.

We have the equation:

`\displaystyle A = A_0 (a)^t`

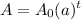
And we would like to determine a.

First, since it is half-life, a=1/2.

Second, since the half-life for our element is 24.3 days, we need to substitute t for t/24.3. This yields:

`\displaystyle A = A_0 ((1)/(2))^(t)/(24.3)`

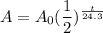
In this way, if t=24.3, then we would have one half-life.

We can rewrite our equation as:

`\displaystyle A = A_0 ((1)/(2)^(1)/(24.3))^t`

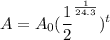
Approximate, rouding to six decimal places. So, our function is:

`A=A_0(0.971878)^t`

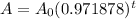
Therefore, our new a is:

`a\approx0.971878`

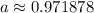
This will give the amount of Phosphorus-32 left after t days, giving the initial amount of A₀.