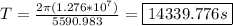Question

A satellite circles the Earth in an orbit whose radius is twice the Earth’s radius. The Earth’s mass is 5.98 x 1024 kg, and its radius is 6.38 x 106 m. What is the period of the satellite?

Answer 1

Hello!

Recall the period of an orbit is how long it takes the satellite to make a complete orbit around the earth. Essentially, this is the same as 'time' in the distance = speed * time equation. For an orbit, we can define these quantities:

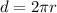`d = 2\pi r` ← The circumference of the orbit

speed = orbital speed, we will solve for this later

time = period

Therefore:

`T = (2\pi r)/(v)`

Where 'r' is the orbital radius of the satellite.

First, let's solve for 'v' assuming a uniform orbit using the equation:

`v = \sqrt{(Gm)/(r)}`

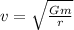
G = Gravitational Constant (6.67 × 10⁻¹¹ Nm²/kg²)

m = mass of the earth (5.98 × 10²⁴ kg)

r = radius of orbit (1.276 × 10⁷ m)

Plug in the givens:

`v = \sqrt{((6.67*10^(-11))(5.98*10^(24)))/((1.276*10^7))} = 5590.983 m/s`

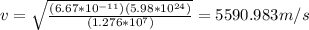
Now, we can solve for the period:

`T = (2\pi (1.276*10^7))/(5590.983) =\boxed{ 14339.776 s}`