Question

The table gives some information about the heights of 30 plants. Height, h in cm Frequency 0​

Answer 1

C (look at explain!)

Explanation:

Answer 2

C. 20 ≤ h < 30

Explanation:

Median

The value in the middle of the data set when all the data values are placed in order of size.

As this is grouped data, we can only estimate the median.

Add an extra row to the table showing the Cumulative Frequency:

`\begin{array}c\cline{1-3} \sf Height & \sf Frequency & \sf Cumulative\:Frequency \\\cline{1-3} \sf 0 \leq h < 10 & 1 & 1 \\\cline{1-3} \sf 10 \leq h < 20 & 9 & 10 \\\cline{1-3} \sf 20 \leq h < 30 & 7 & 17 \\\cline{1-3} \sf 30 \leq h < 40 & 13 & 30 \\\cline{1-3}\end{array}`

To find which class the median is in, divide the total number of data values by 2:

`\implies \sf (n)/(2)=(30)/(2)=15`

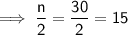
Therefore, there are 15 values less than or equal to the median.

From the table, the 11th to 17th data values are in class 20 ≤ h < 30. Therefore, the median must be in the 20 ≤ h < 30 class.