Question

Which polynomials have 2 roots

Answer 1

Option D

Explanation:

Option A

x² - 3x² + 2x² = 0

Therefore, the given polynomial has no roots.

Option B

x² + 2x + 8

By quadratic formula,

x =
`(-2\pm √(4-32) )/(2)`

=
`(-2\pm √(-28) )/(2)`

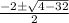
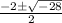
Therefore, roots are imaginary and for a polynomial with degree 1 or more than 1, both the roots can't be imaginary.

So the polynomial can't have exactly two roots.

Option C

99x³ - 33x + 1

Since the polynomial is of degree 3, so it will have three roots.

Therefore, the polynomial will not have exactly 2 roots.

Option D

√2x - 3x² + 7√2

By quadratic formula,

x =
`\frac{-√(2)\pm\sqrt{(√(2))^2-4(-3)(7√(2) )}}{2(-3)}`

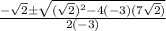
x =
`\frac{-√(2)\pm\sqrt{2+84√(2) )}}{(-6)}`

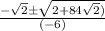
There are exactly two real roots.

Therefore Option D is the answer.

Option E

4x + 11x - 111

Since this polynomial is of a degree 1.

There will be only one root.