Question

A city has a vacant lot in the shape of an isosceles trapezoid and the city workers are installing a fence around the lot. What length of fencing is required? Round the answer to the nearest meter. А 25 m B x 25 m 45° The length of fencing required is meters.​

Answer 1

Length of the fence required = 135 m

Explanation:

Total length of the fence required to cover the vacant lot = Perimeter of the isosceles trapezoid

Perimeter of ABCD = AB + BC + CD + AD

Since, AB = BC = EF = ED = 25 m

From the given right triangle BEC,

m∠EBC = m∠ECB = 45°

ΔBEC will be an isosceles triangle.

So, BE = EC

By Pythagoras theorem,

BC² = BE² + EC²

25² = 2(EC)²

EC =
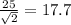`(25)/(√(2)) =17.7` m

And DC = (DF + EF + EC)

= EC + EF + EC [Since, DF = EC]

= 2EC + EF

= 35.4 + 25

= 60.4 m

Hence. perimeter of ABCD = 25 + 25 + 60.4 + 25

= 135.4 m

≈ 135 m

Therefore, length of the fence required = 132 m