Part A: The voltage across the secondary coil is 3 V.
Part B: With a turns ratio of 10, the secondary coil has 10 turns.
Part C: The secondary coil, with 10 turns, decreases the current from 500 A to 25 A.
Part D: The secondary current is 12.5 A.
Part E: The power in the secondary coil is 1600 W.
Part F: The current in the primary coil is 0.5 A.
Part G:The efficiency of the transformer is approximately 8.16%.
Part A:
The voltage across the secondary coil
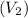 is determined by the turns ratio in a transformer, expressed as
is determined by the turns ratio in a transformer, expressed as
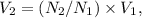 where
where
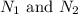 are the number of turns in the primary and secondary coils, respectively, and
are the number of turns in the primary and secondary coils, respectively, and
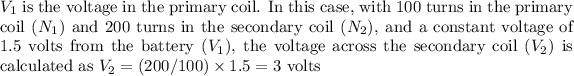 .
.
Part B:
For a transformer intended to reduce the alternating voltage from 500 volts to 25 volts, the turns ratio
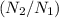 is equal to the voltage ratio (\
is equal to the voltage ratio (\
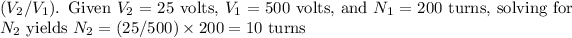 in the secondary coil.
in the secondary coil.
Part C:
In transforming the alternating current from 500 amperes to 25 amperes, the turns ratio is given by
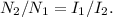 With
With
 amperes,
amperes,
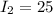 amperes, and
amperes, and
 turns, solving for
turns, solving for
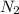 results in
results in
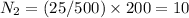 turns in the secondary coil.
turns in the secondary coil.
Part D:
The relationship between the primary current
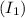 and the secondary
and the secondary
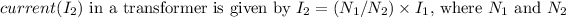 are the number of turns in the primary and secondary coils, respectively. For a transformer with 400 turns in the primary coil
are the number of turns in the primary and secondary coils, respectively. For a transformer with 400 turns in the primary coil
 and 80 turns in the secondary coil
and 80 turns in the secondary coil
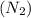 , and a primary current
, and a primary current
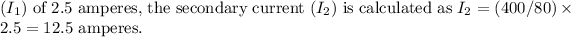
Part E:
The power
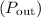 generated in the secondary coil of a transformer can be determined by the turns ratio squared, multiplied by the power supplied to the primary coil
generated in the secondary coil of a transformer can be determined by the turns ratio squared, multiplied by the power supplied to the primary coil
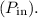 The formula is
The formula is
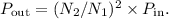 With 200 turns in the primary coil
With 200 turns in the primary coil
 800 turns in the secondary coil
800 turns in the secondary coil
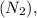 and 400 watts of power supplied to the primary coil
and 400 watts of power supplied to the primary coil
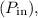 the power generated in the secondary coil is calculated as
the power generated in the secondary coil is calculated as
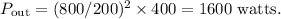
Part F:
In a transformer, the primary current
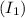 can be determined using the power formula
can be determined using the power formula
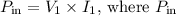 is the power supplied to the transformer,
is the power supplied to the transformer,
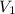 is the voltage in the primary coil, and
is the voltage in the primary coil, and
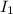 is the current in the primary coil. Given that the power supplied is 60 watts
is the current in the primary coil. Given that the power supplied is 60 watts
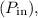 the voltage in the primary coil
the voltage in the primary coil
 s 120 volts, and solving for
s 120 volts, and solving for
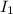 gives
gives

Part G:
The efficiency
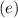 of a transformer is defined as the ratio of the output power
of a transformer is defined as the ratio of the output power
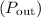 to the input power
to the input power
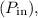 expressed as a percentage
expressed as a percentage
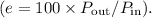 For a nonideal transformer, the given values are: voltage and current in the primary coil
For a nonideal transformer, the given values are: voltage and current in the primary coil
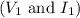 are 120 volts and 2.0 amperes, respectively; voltage and current in the secondary coil
are 120 volts and 2.0 amperes, respectively; voltage and current in the secondary coil
 are 19.4 volts and 11.8 amperes, respectively.
are 19.4 volts and 11.8 amperes, respectively.
