Question

The hands of the clock in the tower of the Houses of Parliament in London are approximately 3m and 2.5m. How fast is the distance between the tips of the hands changing at 9:00?

Answer 1

`(dc)/(dt)=11.05 m/hr`

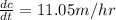
Explanation:

Using the low of cosine we have:

`c^2=a^2+b^2-2abcos(\theta)`

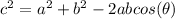
Here:

a is 3 m

b is 2.5

c is the distance between the tips of the hands

Solving this equation for cos(θ) we have:

`cos(\theta)=(3^2+2.5^2-c^2)/(2*3*2.5)`

`cos(\theta)=(15.25-c^2)/(15)`

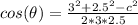
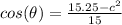
Now we need to take the derivative with respect to time (t) on each side of the equation.

`-sin(\theta)(d\theta)/(dt)=(1)/(15)(-2c(dc)/(dt))`

`sin(\theta)(d\theta)/(dt)=(2c)/(15)((dc)/(dt))`

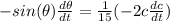
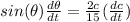
Here dc/dt represents how fast the distance between the tips changes.

Now, we need to find the variation of the angle with respect to time.

The minute hand angle covers 360° in 1 hour and the hour hand 30° in 1 hour, therefore the covers angle between the tips in one hour will be 360-30=330° or dθ/dt = 330°/hr = 5.76 rad/hr.

On the other hand, we can find c at 9:00. In this case, we have a right triangle. Let's see that the angle between the hands at this time is 90° so sin(90)=1

`c=√(3^2+2.5^2)=3.91 m`

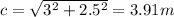
Putting all of this in our equation we have:

`sin(90)5.76=(2*3.91)/(15)((dc)/(dt))`

`5.76=(2*3.91)/(15)((dc)/(dt))`

`(5.76*15)/(2*3.91)=((dc)/(dt))`

`((dc)/(dt))=11.05 m/hr`

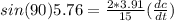
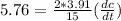
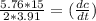
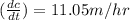
Therefore the rate change of the tips will be 11.05 m/hrs.

I hope it helps you!