Answer:
x =
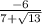
r =
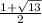
Explanation:
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-one number called the common ratio.
For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2.
-----
Let's take r=ratio of the geometric sequence
in first term, x is multiplied by
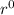
First term: x
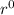
Second term: 4x+3 = x
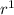
Third term: 7x+3 = x
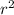
From the last 2 equation, we have to obtain r and x values.
Second equation - First equation:
3x = x r (r - 1)
Let's state: x different from 0, so we can simplify x, obtaining:
3 =
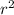 - r
- r
0 =
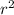 - r - 3
- r - 3
r =
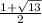 (only the positive value of r counts)
(only the positive value of r counts)
so, going to second term of the sequence:
4x+3 = x
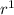 => x (4 -
=> x (4 -
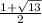 ) = -3
) = -3
x (
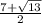 ) = -3 => x =
) = -3 => x =
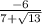
hope it helps..