Question

A straight line has gradient 4 and passes through the point (5,23).

Work out the equation of the line.

Answer 1

Equation of line is:
`\mathbf{y=4x+3}`

Explanation:

We are given:

A straight line has gradient 4 and passes through the point (5,23).

Work out the equation of the line.

The equation of line will be in slope-intercept form:
`y=mx+b`

where m is slope and b is y-intercept

Finding slope

We have slope (gradient) m = 4

Finding y-intercept

Using slope m = 4 and point (5,23) we can find b i.e y-intercept

`y=mx+b\\23=4(5)+b\\23=20+b\\b=23-20\\b=3`

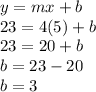
So, we get y-intercept b = 3

Finding Equation of Line

Now, writing equation of line having slope m = 4 and y-intercept b = 3 is:

`y=mx+b\\y=4x+3`

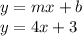
So, the Equation of line is:
`\mathbf{y=4x+3}`