Answer:
The angle subtended by the arc is 171.8873385 degrees (3 radians)
Explanation:
The formula of the length of an arc of a sector is L =
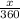 × 2 π r, where
× 2 π r, where
- x is the central angle subtended by the arc
- r is the radius of the circle
∵ An arc of a sector is three times its radius
∴ L = 3r
→ Equate the formula of the length of the arc by 3r
∵
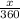 × 2 π r = 3r
× 2 π r = 3r
→ Divide both sides by r
∴
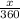 × 2 π = 3
× 2 π = 3
→ Simplify the left side
∵
 x = 3
x = 3
→ Divide both sides by

∴ x = 171.8873385°
∴ The angle subtended by the arc is 171.8873385 degrees (3 radians)