Question

Integrate the following:

`\displaystyle \int (x^2)/(x^2+x+3)\, dx`

Answer 1

hope this will help you........

Answer 2

`\int {(x^2)/(x^2+x+3) } \, dx = - (5√(11) )/(11)arctan((√(11)(2x+1) )/(11) ) - (1)/(2)ln|x^2+x+3| +x + C`

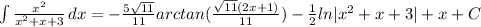
General Formulas and Concepts:

Pre-Algebra

• Distributive Property

Algebra I

• Completing the Square
• Rearranging Variables

Algebra II

• Long Division

Calculus

• U-Substitution
• [Integration Trick 1] Numerator Split
• [Integration Trick 2] Completing the Square
• Integration Rule 1:
  `\int {cf(x)} \, dx = c\int {f(x)} \, dx`
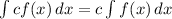
• Integration Rule 2:
  `\int {f(x)+g(x)} \, dx =\int {f(x)} \, dx + \int {g(x)} \, dx`
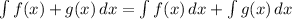
• Integration 1:
  `\int {(1)/(u) } \, du =ln|u| + C`
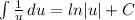
• Integration 2:
  `\int {(du)/(u^2+a^2) } = (1)/(a) arctan((u)/(a) )+C`
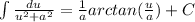
• Integration 3:
  `\int {x^n} \, dx = (x^(n+1))/(n+1) +C`

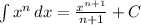
Explanation:

Step 1: Define

`\int {(x^2)/(x^2+x+3) } \, dx`

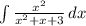
Step 2: Simplify Function

We do long division to simplify the function inside the function.

See Attachment for Long Division Work.

Once we do long division, our function becomes
`1-(x+3)/(x^2+x+3)`

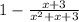
Now we rewrite our Integral:
`\int ({1-(x+3)/(x^2+x+3) }) \, dx`

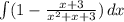
Step 3: Integrate Pt. 1

1. Distributive Integral [Int Rule 1]:
   `\int {1} \, dx - \int {(x+3)/(x^2+x+3) } \, dx`
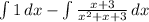
2. Integrate 1st Integral [Int 3]:
   `x - \int {(x+3)/(x^2+x+3) } \, dx`

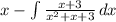
Step 4: Identify Variables Pt.1

Set variables for u-substitution.

u = x² + x + 3

du = (2x + 1)dx

Step 5: Integrate Pt. 2

1. Rewrite Integral [Int Rule 1]:
   `x - (1)/(2) \int {(2(x+3))/(x^2+x+3) } \, dx`
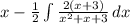
2. Distribute 2 [Alg]:
   `x - (1)/(2) \int {(2x+6)/(x^2+x+3) } \, dx`
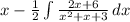
3. Rewrite Integral [Alg]:
   `x - (1)/(2) \int {(2x+1+5)/(x^2+x+3) } \, dx`
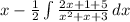
4. Rewrite Integral [Int Trick 1]:
   `x - (1)/(2) [\int {(2x+1)/(x^2+x+3) } \, dx + \int {(5)/(x^2+x+3) } \, dx ]`
5. (2nd Int) Complete the Square:
   `x - (1)/(2) [\int {(2x+1)/(x^2+x+3) } \, dx + \int {(5)/((x+(1)/(2))^2 + (11)/(4) ) } \, dx ]`

Step 6: Identify Variables Pt. 2

Set variables for u-substitution for 2nd integral.

z = x + 1/2

dz = dx

a = √(11/4)

Step 7: Integrate Pt. 3

1. [Integrate] U-Substitution:
   `x - (1)/(2) [\int {(1)/(u) } \, du + \int {\frac{5}{z^2 + (\sqrt{(11)/(4)})^2} } \, dz ]`
2. Rewrite Integral [Int Rule 1]:
   `x - (1)/(2) [\int {(1)/(u) } \, du + 5\int {\frac{dz}{z^2 + (\sqrt{(11)/(4)})^2} } ]`
3. Integrate 1st Integral [Int 1]:
   `x - (1)/(2) [ln|u| + 5\int {\frac{dz}{z^2 + (\sqrt{(11)/(4)})^2} } ]`
4. Integrate 2nd Integral [Int 2]:
   `x - (1)/(2) [ln|u| + 5(\frac{1}{\sqrt{(11)/(4)}}arctan(\frac{z}{\sqrt{(11)/(4) } } ) ) ]`
5. Distribute 5 [Alg]:
   `x - (1)/(2) [ln|u| + \frac{5}{\sqrt{(11)/(4)}}arctan(\frac{z}{\sqrt{(11)/(4) } } ) ]`
6. Distribute -1/2 [Alg]:
   `x - (1)/(2)ln|u| - \frac{5}{2\sqrt{(11)/(4)}}arctan(\frac{z}{\sqrt{(11)/(4) } } )`
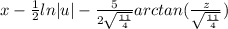
7. Rationalize [Alg]:
   `x - (1)/(2)ln|u| - (5√(11) )/(11)arctan(\frac{z}{\sqrt{(11)/(4) } } )`
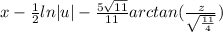
8. Resubstitute variables [Alg]:
   `x - (1)/(2)ln|x^2+x+3| - (5√(11) )/(11)arctan(\frac{x+(1)/(2) }{\sqrt{(11)/(4) } } )`
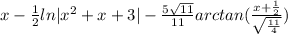
9. Simplify/Rationalize [Alg]:
   `x - (1)/(2)ln|x^2+x+3| - (5√(11) )/(11)arctan((√(11)(2x+1) )/(11) )`
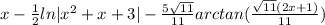
10. Rewrite [Alg]:
    `- (5√(11) )/(11)arctan((√(11)(2x+1) )/(11) ) - (1)/(2)ln|x^2+x+3| +x`
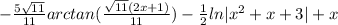
11. Integration Constant:
    `- (5√(11) )/(11)arctan((√(11)(2x+1) )/(11) ) - (1)/(2)ln|x^2+x+3| +x + C`

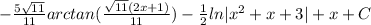
And we have our final answer! Hope this helped you on your Calculus Journey!