Question

Based on a sample of 150 textbooks at the store, you find an average of 70.69 and a standard deviation of 29.6. The point estimate is: Incorrect (to 3 decimals) The 99 % confidence interval (use z*) is:______

Answer 1

Explanation:

Given that:

The sample size = 150

The sample mean = 70.69

The standard deviation = 29.60

The sample mean is equal to the point estimate of the population = 70.69

At 99% confidence interval level is:

∝ = 1 - 0.99

∝ = 0.01

The critical value:

`Z_(\alpha/2) = Z_(0.01/2) \\ \\ Z_(0.005) = 2.58 \ using \ Z \ tables`

The Margin of error =
`Z_(\alpha/2) * (\sigma)/(√(n))`

`= 2.58 * (29.6)/(√(150))`

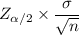
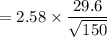
= 2.58 × 2.4168

≅ 6.235

At 99% confidence interval; the estimate of the population mean lies within the interval:

=
`\overline x - E < \mu \ < \overline x + E`

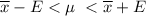
= 70.69 - 6.235 < μ < 70.69 + 6.235

= 64.455 < μ < 76.925

= (64.455 , 76.925 )