Answer:
0.426 volts
Step-by-step explanation:
It is given that,
The radius of a circular loop, r = 11.2 cm = 0.112 m
An elastic conducting material is stretched into a circular loop.
It is placed with its plane perpendicular to a uniform 0.880 T magnetic field.
The radius of the loop starts to shrink at an instantaneous rate of 68.8 cm/s, dr/dt = 0.688 m/s
We need to find the emf induced in the loop at that instant.
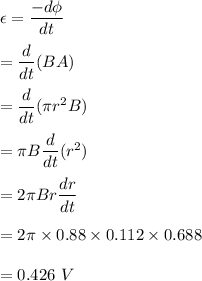
So, the magnitude of induced emf is 0.426 volts.