Answer:
See proof below
Explanation:
Important points
- understanding what it means to be "onto"
- the nature of a quadratic function
- finding a value that isn't in the range
Onto
For a function with a given co-domain to be "onto," every element of the co-domain must be an element of the range.
However, the co-domain here is suggested to be
 , whereas the range of f is not
, whereas the range of f is not
 (proof below).
(proof below).
Proof (contradiction)
Suppose that f is onto
 .
.
Consider the output 7 (a specific element of
 ).
).
Since f is onto
 , there must exist some input from the domain
, there must exist some input from the domain
 , "p", such that f(p) = 7.
, "p", such that f(p) = 7.
Substitute and solve to find values for "p".
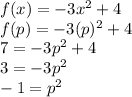
Next, apply the square root property:

By definition,
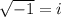 , so
, so
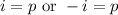
By the Fundamental Theorem of Algebra, any polynomial of degree n with complex coefficients, has exactly n complex roots. Since the degree of f is 2, there are exactly 2 roots, and we've found them both, so we've found all of them.
However, neither
 nor
nor
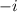 are in
are in
 , so there are zero values of p in
, so there are zero values of p in
 for which f(p)= 7, which is a contradiction.
for which f(p)= 7, which is a contradiction.
Therefore, the contradiction supposition must be false, proving that f is not onto
