Hii!
___________________________________________________________
Answer:
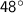
Explanation:
The sum of complementary angles is always 90 degrees.
We can find the complement of 90 by setting up an equation; (let x be the unknown angle).
 42+x=90
42+x=90
Subtract 42 from both sides
x=48
--
Hope that this helped! Best wishes.
--