Answer:
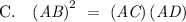
Explanation:
This problem uses the concept of the tangent-secant theorem which describes the relationship of the segments a secant line and a tangent line with the associated circle. This theorem is found as Proposition 36 in Book 3 of Euclid's Elements.
As shown in the figure attached below, segment AB (in blue) forms a tangent with the circle BCD and segment AD (in orange) is the secant where it intersects the circle at point C.
Furthermore, let two segments (in green) be drawn one from point C and point D.
To show that
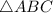 is similar to
is similar to
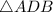 , notice that both triangles share a common angle
, notice that both triangles share a common angle
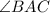 . Additionally, by the alternate segment theorem,
. Additionally, by the alternate segment theorem,
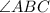 is equal to
is equal to
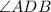 . Therefore,
. Therefore,
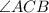 is also equal to
is also equal to
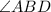 .
.
Hence,
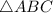 is indeed similar to
is indeed similar to
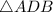 . This implies the ratio of the sides of both triangles is the same. Particularly,
. This implies the ratio of the sides of both triangles is the same. Particularly,
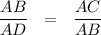 .
.
Then, performing cross multiplication yields
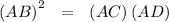 .
.
Therefore, the product of the lengths of the secant segment and its external segment is equal to the square of the length of the tangent segment.