Question

F the distance separating the objects is the same for each pair, which pair of objects will have the greatest gravitational force between them? a 50-kg object and an 80-kg object a 65-kg object and a 65-kg object a 65-kg object and a 75-kg object a 60-kg object and a 70-kg object

Answer 1

A 65-kg object and an 75-kg object.

Step-by-step explanation:

The gravitational force is given by :

`F=G(m_1m_2)/(r^2)`

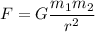
F is directly proportional to the product of masses and inversely to the distance between them.

In this problem, the distance separating the objects is same for each pair. We need to find the greatest gravitational force between them.

(1) a 50-kg object and an 80-kg object

`F_1=G(4000)/(r^2)\ N`

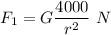
(2) a 65-kg object and an 65-kg object

`F_2=G(4225)/(r^2)\ N`

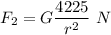
(3) a 65-kg object and an 75-kg object

`F_3=G(4875)/(r^2)\ N`

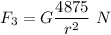
(4) a 60-kg object and an 70-kg object

`F_4=G(4200)/(r^2)\ N`

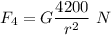
From the above calculations we find that if the product of masses is maximum, it lead to maximum gravitational force between objects. Hence, a 65-kg object and an 75-kg object will have maximum gravitational force between them.