Question

Choose the answer that validates that the rate of change is constant by showing that the ratios of the two quantities are proportional and equivalent to the unit rate (simplified constant rate of change): NUMBER OF TEXTBOOKS Number of Students Number of Textbooks 7 35 14 70 21 105 28 140

Answer 1

Given:

The table of values is

Number of Students : 7 14 21 28

Number of Textbooks : 35 70 105 140

To find:

The rate of change and showing that the ratios of the two quantities are proportional and equivalent to the unit rate.

Solution:

The ratio of number of textbooks to number of students are

`(35)/(7)=5`

`(70)/(14)=5`

`(105)/(21)=5`

`(140)/(28)=5`

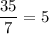
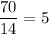
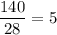
All the ratios of the two quantities are proportional and equivalent to the unit rate.

Let y be the number of textbooks and x be the number of students, then

`(y)/(x)=k`

Here, k=5.

`(y)/(x)=5`

`y=5x`

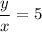
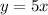
Hence the rate of change is constant that is 5.