Question

Use the Discriminant to find the number and type of solutions to x^2 + 6x -5 = 4x^2

A 2 Real Solutions
B 1 Real Solution
C Real Solutions, 2 Imaginary Solutions
D 3 Solution

Answer 1

The equation
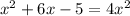`x^2 + 6x -5 = 4x^2` have 2 non-real solution, 2 imaginary solutions.

Explanation:

Using the Discriminant to find the number and type of solutions to
`x^2 + 6x -5 = 4x^2\\x^2-4x^2+6x-5=0\\-3x^2+6x-5=0`

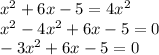
The discriminant is:
`b^2-4ac`

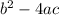
We have a = -3, b=6 and c=-5

Putting values and finding discriminant

`b^2-4ac\\=(6)^2-4(-3)(-5)\\=36-60\\=-24\\`

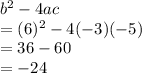
So, we get discriminant = -24

if discriminant < 0 the solution will have two non-real imaginary solutions.

In our case discriminant < 0 i,e discriminant = -24

So, The equation
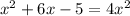`x^2 + 6x -5 = 4x^2` have 2 non-real solution, 2 imaginary solutions.