Question

what are the x-intercept(s) of the function

Answer 1

Zeros of Rational Functions

To find the zeros of a rational function, we must identify values of x that make the numerator equal to 0. We can do this by factoring and by keeping in mind the zero-product property.

The zero-product property states that if the product of two terms is 0, then one of the terms must be equal to 0.

Solving the Question

We're given:

`f(x)=(4x^2-36x)/(x-9)`

First, factor 4x out of the numerator:

`f(x)=(4x(x-9))/(x-9)`

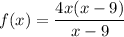
Let f(x) = 0:

`0=(4x(x-9))/(x-9)`

In this case, either x or (x-9) is equal to zero, as they are the two terms being multiplied in the numerator to get 0 as a product.

This makes the x-intercepts of this function 0 and 9.

However, the denominator in this function is x - 9. If x = 9, then it would make the denominator 0, which is not allowed. Therefore, x cannot equal 9, and the only x-intercept is 0.

Answer

x = 0