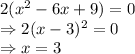Question

The function Q(x)=2x^2-kx+18. For what value of k does Q(x) have one distinct real solution? (NEEDS TO BE DONE WITHIN 2 HOURS!)

Answer 1

k = 12

Explanation:

Given:

The equation
`Q(x)=2x^2-kx+18`

To find:

Value of
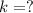`k = ?` for which the given equation has one distinct real solution.

Solution:

The given equation is a quadratic equation.

There are always two solutions of a quadratic equation.

For the equation:
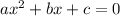`ax^(2) +bx+c=0` to have one distinct solution:

`b^2 - 4ac = 0`

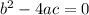
Here,

a = 2,

b = -k and

c = 18

Putting the values, we get:

`(-k)^2 - 4* 2* 18 = 0\\\Rightarrow k^2 = 18* 8\\\Rightarrow k^2 =144\\\Rightarrow k = 12`

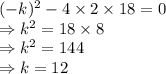
The equation becomes:

`Q(x)=2x^2-12x+18`

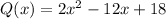
And the one root is:

`2(x^2-6x+9 ) = 0\\\Rightarrow 2(x-3)^2=0\\\Rightarrow x = 3`