Question

Determine slope of any line perpindicular to GH. (-1,2) (-2,-1)

Answer 1

Perpendicular slope = – 1/m = -1/3 = -1/3

Explanation:

Given the points

• (-1,2)

• (-2,-1)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-1,\:2\right),\:\left(x_2,\:y_2\right)=\left(-2,\:-1\right)`

`m=(-1-2)/(-2-\left(-1\right))`

`m=(-1-2)/(-2-\left(-1\right))`

`m=3`

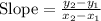
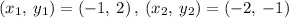
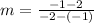
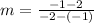
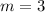
We know that a line perpendicular to another line contains a slope that is the negative reciprocal of the slope of the other line, such as:

slope = m = 3

perpendicular slope = – 1/m = -1/3 = -1/3

Thus, the slope of any line perpendicular to GH = -1/3