Question

. Emily pushes a 38.8 kg grocery cart of groceries by exerting a 76.0 N force on the handle inclined at 40.0 degrees below the horizontal. What are:

a. The horizontal and vertical components of Emily’s force






b. The acceleration of the cart?

Answer 1

a)
`F_(x) = 58.2 N`

`F_(y) = 48.9 N`

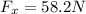
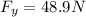
b) a = 1.5 m/s²

Step-by-step explanation:

a) The horizontal and vertical components of Emily's force can be found knowing the angle and the exerted force.

Since the handle is inclined at 40.0° below the horizontal we have:

`F_(x) = |F|*cos(\theta) = 76.0 N*cos(40) = 58.2 N`

`F_(y) = |F|*sin(\theta) = 76.0 N*sin(40) = 48.9 N`

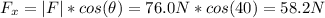
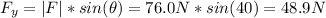
b) The acceleration of the car can be calculated as follows:

`F_(x) = ma`

We used the horizontal component of the force because the cart is moving in that direction.

`a = (F_(x))/(m) = (58.2 N)/(38.8 kg) = 1.5 m/s^(2)`

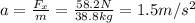
Hence, the acceleration of the car is 1.5 m/s².

I hope it helps you!