Question

HELP ANSWER FOR 30 POINTS

A cone has a volume of 24 cubic inches. What is the volume of a cylinder that the cone fits exactly inside of? ​

Answer 1

`V_(cylinder)=72\:in^3`

Explanation:

• 
  `V_(cone)=24\: in^3` (Given)

• It is given that: Cone fits exactly inside the cylinder.

• 
  `\implies V_(cylinder)=3*V_(cone)`

• 
  `\implies V_(cylinder)=3*24`

• 
  `\implies V_(cylinder)=72\:in^3`

Answer 2

Answer: 72 cubic inches

Explanation:

The formula for the volume of a cone:
`(1)/(3)\pi r^(2)h`

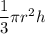
Formula for the volume of a cylinder:
`\pi r^(2)h`

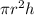
We are given that a cylinder should fit exactly inside the cone

Upon comparing the two equations above, we get:

`$$Volume of cone = (1)/(3)\text{Volume of cylinder}`

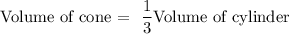
Since we are given the volume of cone is 24 cubic inches, we can write down the below:

`24 = (1)/(3)\text{Volume of cylinder }\\ \text{Volume of cylinder = 72 cubic inches}`

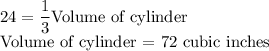
Therefore, we can conclude that if the volume of the cylinder is 72 cubic inches, then the cone with volume of 24 cubic inches can fit exactly in.