Answer: 1. halve
2. halve
3. double
Step-by-step explanation:
The relationship between wavelength and energy of the wave follows the equation:

E= energy
 = wavelength of the wave
= wavelength of the wave
h = Planck's constant
c = speed of light
Thus as wavelength and energy have inverse realation, when wavelength will halve , energy will double.
2. The between wavenumber and energy of the wave follows the equation:
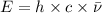
E= energy
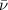
 = wavenumber of the wave
= wavenumber of the wave
h = Planck's constant
c = speed of light
Thus as wavenumber and energy have direct relation, when wavenumber will halve , energy will be halved.
3. The relationship between energy and frequency of the wave follows the equation:
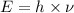
where
E = energy
h = Planck's constant
 = frequency of the wave
= frequency of the wave
Thus as frequency and energy have direct realation, when frequency will double , energy will double.