Question

A rocket with total mass 3.00 3 105 kg leaves a launch pad at Cape Kennedy, moving vertically with an acceleration of 36.0 m/s2. If the speed of the exhausted gases is 4.50 3 103 m/s, at what rate is the rocket initially burning fuel?

(a) 3.05 3 103 kg/s
(b) 2.40 3 103 kg/s
(c) 7.50 3 102 kg/s
(d) 1.50 3 103 kg/s
(e) None of these

Answer 1

(b) 2.40 x
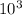`10^(3)` kg/s

Step-by-step explanation:

Given that: Total mass of the rocket = 3.003 x
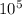`10^(5)` kg

acceleration of the rocket = 36.0 m
`s^(-2)`

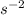
speed of the exhausted gases = 4.503 x
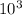`10^(3)` m/s

Rate at which rocket was initially burning fuel =
`(mass)/(time)`

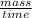
But,

time =
`(velocity)/(acceleration)`

=
`(4.503*10^(3) )/(36.0)`

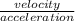
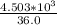
= 125.0833 s

So that;

Rate at which rocket was initially burning fuel =
`(3.003*10^(5) )/(125.0833)`

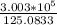
= 2400.8001

= 2.40 x
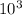`10^(3)` kg/s

Therefore, the initial rate at which the rocket burn fuel is 2.40 x
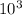`10^(3)` kg/s.