Answer:
The daily rate that maximizes the revenue is $40 and the maximum revenue is $9600
Explanation:
Given
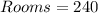
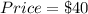
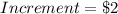
First, we calculate the revenue.

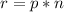
Let x be the change in rate.
i.e.
For every 2x increment in price (p) i.e. p + 2x
There will be 4 fewer rooms (n) i.e. n - 4x
So, the revenue is updated as:

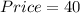
So:
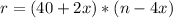
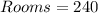
So:
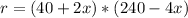
Expand
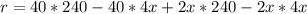
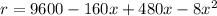
Reorder
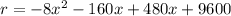
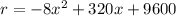
The maximum of a function is calculated as:

In:
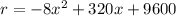
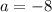
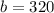

So:

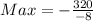
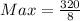
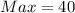
To get the maximum revenue;
Substitute 40 for x in
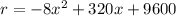
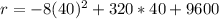
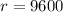
The daily rate that maximizes the revenue is $40 and the maximum revenue is $9600