Question

The sum of the first five terms of an arithmetic sequence is 35. The sum of the next five terms is 85. Determine the first term and the common difference of the sequence.

Answer 1

The first term is 3 and the common difference is 2

Explanation:

The formula of the sum of the nth term of the arithmetic sequence is

`S_(n)=(n)/(2)[2a+(n-1)d]`, where

• a is the first term

• d is the common difference

• n is the position of the term

∵ The sum of the first five terms of an arithmetic sequence is 35

∴
`S_(5)` = 35

→ Substitute The values of n and S in the rule above

∵ 35 =
`(5)/(2)[2a+(5-1)d]`

∴ 35 =
`(5)/(2)[2a+4d]`

→ Simplify the right side

∴ 35 = 5a + 10d

→ Switch the two sides

∴ 5a + 10d = 35 ⇒ (1)

∵ The sum of the next five terms is 85

→ To find the sum of the first 10 terms add 85 to
`S_(5)`

∴
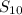`S_(10)` = 35 + 85 = 120

→ Substitute The values of n and S in the rule above

∵ 120 =
`(10)/(2)[2a+(10-1)d]`

∴ 120 = 5[2a + 9d]

→ Simplify the right side

∴ 120 = 10a + 45d

→ Switch the two sides

∴ 10a + 45d = 120 ⇒ (2)

Now we have a system of equations to solve it and find a and d

→ Multiply equation (1) by -2

∵ -2(5a) + -2(10d) = -2(35)

∴ -10a + -20d = -70 ⇒ (3)

→ Add equations (2) and (3)

∵ (10a + -10a) + (45d + -20d) = (120 + -70)

∴ 25d = 50

→ Divide both sides by 25 to find d

∴ d = 2

→ To find a substitute d in equation (1) by 2

∵ 5a + 10(2) = 35

∴ 5a + 20 = 35

→ Subtract 20 from both sides

∵ 5a + 20 - 20 = 35 - 20

∴ 5a = 15

→ Divide both sides by 5

∴ a = 3

∴ The first term is 3 and the common difference is 2