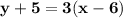Question

HELPPP ITS AN EMERGENCY!!!!!!

Answer 1

The equation in point-slope is
`\mathbf{y+5=3(x-6)}`

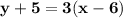
Explanation:

We need to write the point-slope form of the equation of the line passing through the point (6,-5) and perpendicular to the line
`y=-(1)/(3)x+4`

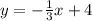
The general form of point-slope is;
`y-y_1=m(x-x_1)`

where m is slope and
`(x_1,y_1)` is the point

We need to calculate slope.

We are given equation of line
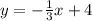`y=-(1)/(3)x+4` that is perpendicular to the required line.

The equation is given in slope-intercept form
`y=mx+b` where m is slope.

Comparing both equations we get m= -1/3

But we know that when lines are perpendicular their slopes are opposite reciprocal of each other i.e
`m=-(1)/(m)`

So, slope of required line is m = 3 (opposite reciprocal of -1/3)

Now, the equation in point-slope form having slope m=3 and point (6,-5) is

`y-y_1=m(x-x_1)\\y-(-5)=3(x-6)\\y+5=3(x-6)`

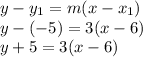
So, The equation in point-slope is
`\mathbf{y+5=3(x-6)}`