Question

Write the equation of the line that passes through (5, 6) and (8, 4) in slope-intercept form.

Answer 1

Explanation:

Equation of the line in slope- intercept form:

`\sf \boxed{\bf y = mx +b}`

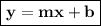
Here, m is the slope and b is the y-intercept

Find the slope with the given two points.

`\sf \boxed{slope = (y_2-y_1)/(x_2-x_1)}`

`\sf =(4-6)/(8-5)\\\\=(-2)/(3)`

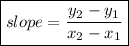
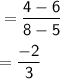
Slope = -2/3 and choose any one the given points.

Substitute m = -2/3 and (5,6) in the above equation and find 'b'

`\sf 6 =(-2)/(3)*5+b\\\\6 =(-10)/(3)+b\\\\6+(10)/(3)=b\\\\(6*3)/(1*3)+(10)/(3)=b\\\\(18)/(3)+(10)/(3)=b\\\\\boxed{b=(28)/(3)}`

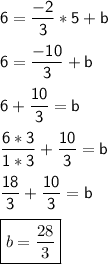
Equation of the line:

`y = (-2)/(3)x + (28)/(3)`