Question

Review the graph of complex number z.

On a coordinate plane, the y-axis is labeled imaginary and the x-axis is labeled real. Point z is at (negative 6, 6).

What is the polar form of z?

6 StartRoot 2 EndRoot(cos(135°) + isin(135°))
6 StartRoot 3 EndRoot(cos(135°) + isin(135°))
6 StartRoot 2 EndRoot(cos(225°) + isin(225°))
6 StartRoot 3 EndRoot(cos(225°) + isin(225°))

Answer 1

9514 1404 393

Answer:

`6√(2) (\cos(135^(\circ))+i\sin(135^(\circ)))`

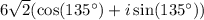
Explanation:

The angle to the point in the second quadrant is measured from the positive real axis (the x-axis). Second quadrant angles are between 90° and 180°, leaving the 135° choices as the only ones that make sense.

The magnitude of z is the root of the sum of the squares of its components:

|z| = √((-6)^2 +6^2) = 6√2

So, the polar form of z is ...

`\boxed{6√(2) (\cos(135^(\circ))+i\sin(135^(\circ)))}`

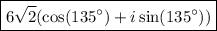
this matches the first choice