Question

If there are 180 grams of radioactive material with a half-life (decrease by half or 50%) of 1 hour, how much of the radioactive material will be left after 3 hours?

Answer 1

After 3 hours there is left 22.5 grams of radioactive material.

Explanation:

We can calculate the mass of radioactive material remaining after 3 hours, by using the decay equation:

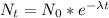`N_(t) = N_(0)*e^(-\lambda t)` (1)

Where:

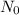`N_(0)`: is the initial mass = 180 g

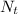`N_(t)`: is the remaining mass after time t

λ: is the decay constant

The decay constant is given by:

`\lambda = (ln(2))/(t_(1/2))`

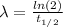
Where
`t_(1/2)` = 1 h.

By entering λ into equation (1) we hve:

`N_(t) = N_(0)*e^{-(ln(2))/(t_(1/2)) t}`

`N_(t) = 180 g*e^{-(ln(2))/(1 h) 3 h} = 22.5 g`

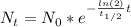
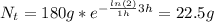
Therefore, after 3 hours there is left 22.5 grams of radioactive material.

I hope it helps you!