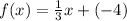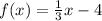Question

What is the linear function equation represented by the graph?

Graph of a line on a coordinate plane. The horizontal x-axis ranges from negative 5 to 5 in increments of 1. The vertical y-axis ranges from negative 5 to 5 in increments of 1. A line intersects the y-axis at begin ordered pair 0 comma negative 4 end ordered pair and passes through at begin ordered pair 3 comma negative 3 end ordered pair.



Enter your answer in the box.

f(x)=

Answer 1

`f(x) = (1)/(3)x - 4`

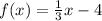
Explanation:

The linear function equation that could represented by the graph can be written in the slope-intercept form, as
`f(x) = mx + b`

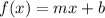
Where,

m = slope of the graph = rise/run

b = y-intercept = the point where the line intercepts the y-axis. At this point, x = 0.

Let us find the values of m and b respectively.

Using two points, (3, -3) and (0, -4),

`slope (m) = (y_2 - y_1)/(x_2 - x_1) = (-4 -(-3))/(0 - 3) = (-1)/(-3) = (1)/(3)`

m = ⅓.

The y-axis is intercepted at y = -4, when x = 0.

Therefore,

b = -4 (y-intercept)

Substitute b = -4, and m = ⅓ into
`f(x) = mx + b`

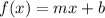
The linear function equation would be:

`f(x) = (1)/(3)x + (-4)`

`f(x) = (1)/(3)x - 4`