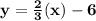Question

Plz help i need this answer to pass

Answer 1

The equation in slope-intercept form of required line is:
`\mathbf{y=(2)/(3)(x)-6}`

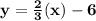
Explanation:

We need to write equation in slope-intercept form to represent the line on the graph.

The general equation in slope-intercept form is:
`y=mx+b`

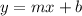
Where m is slope and b is y-intercept

Finding slope using formula:
`Slope=(y_2-y_1)/(x_2-x_1)\\`

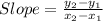
Looking at he graph we have

`x_1=3, y_1=-4, x_2=6, y_2=-2`

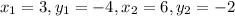
Putting values in formula and finding slope:

`Slope=(-2-(-4))/(6-3)\\\\Slope=(-2+4)/(3)\\Slope=(2)/(3)`

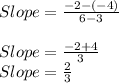
So, we get slope m = 2/3

Using slope m=2/3 and point (3,-4) we can find y-intercept

`y=mx+b\\\\-4=(2)/(3)( 3)+b\\-4=2+b\\b=-4-2\\b=-6`

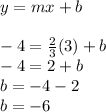
So, y-intercept b = -6

The equation of line having m=2/3 and b=-6 will be:

`y=mx+b\\y=(2)/(3)(x)-6`

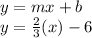
The equation in slope-intercept form of required line is:
`\mathbf{y=(2)/(3)(x)-6}`