Answer:
B. Bending her knees will make the force 20 times smaller.
Step-by-step explanation:
By the Impulse Theorem, we notice that the normal force from the ground to the gymnast counteract the intial linear momentum of the gymnast during a certain time until rest is reached. The impulse (
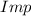 ), measured in newton-second, is function of initial linear momentum, measured in kilogram-meters per second, only and, hence, remains constant. That is:
), measured in newton-second, is function of initial linear momentum, measured in kilogram-meters per second, only and, hence, remains constant. That is:
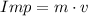 (1)
(1)
Where:
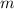 - Mass of the gymnast, measured in kilograms.
- Mass of the gymnast, measured in kilograms.
 - Initial speed of the gymnast, measured in meters per second.
- Initial speed of the gymnast, measured in meters per second.
If we know that
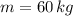 and
and
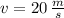 , the impulse experimented by the gymnast is:
, the impulse experimented by the gymnast is:
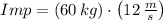
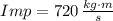
If the time of collision is increased by a factor of 20 by bending her knees, then normal force from the ground on the gymnast must be decrased by a factor of 20 in order to keep the impulse constant.
Therefore, the right answer is B.