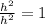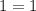Explanation:
Let simplify the identity
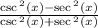
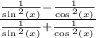
Combine Like Fractions
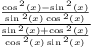
Multiply by reciprocals.
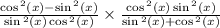
Pythagorean Identity
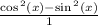
Double Angle Identity
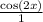
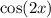
Now, we need to find cos 2x. Given that we have tan x.
Note that
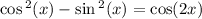
So let find cos x and tan x.
We know that
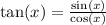
We know that
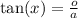
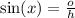
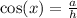
So naturally,
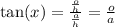
So we need to find the hypotenuse,
remember Pythagorean theorem.
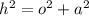
Here o is 1
h is root of 5.
So
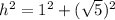
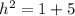
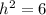
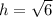
Now, we know h, let plug in to find sin x and cos x.
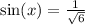
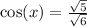
Let's find these values squared
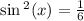
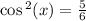
Finally, use the trig identity
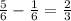
So part I.= 2/3
ii. Use the definition of sine and cosine and Pythagorean theorem
Let sin x= o/h
Let cos x= a/h.
So
sin x squared is
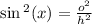
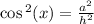
By definition,
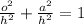
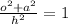
Remember that
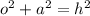
So