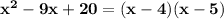Answer:
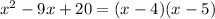
Explanation:
Factoring a Trinomial
A second-degree trinomial can be expressed as:
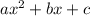
It can be factored, i.e., converted to a product instead of a sum of terms in several ways.
We'll use the grouping method.
Factor:
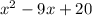
Split the second term into two terms:
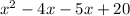
Factor x on the first two terms and -5 on the last two terms:

Now factor out x-4:
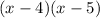
Thus: