Answer:
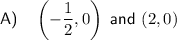
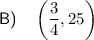
C) see explanation
Explanation:
Given function:
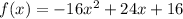
Part A
To find the x-intercepts, set the function to zero, factor and solve for x:
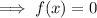
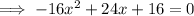
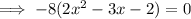
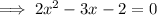
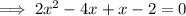
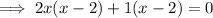
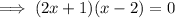
Therefore:
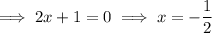
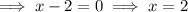
Therefore, the x-intercepts of the graph of f(x) are
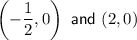
Part B
As the leading coefficient is negative, the parabola will open downwards. Therefore, the vertex of the graph of f(x) will be a maximum.
The x-coordinate of the vertex is the midpoint of the x-intercepts:
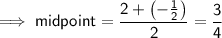
To find the y-coordinate of the vertex, substitute the x-value into the function:
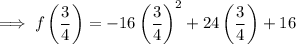
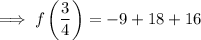
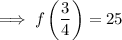
Therefore, the coordinates of the vertex are:
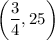
Part C
Find the y-intercept by substituting x = 0 into the function:
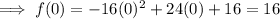
Therefore, the y-intercept is (0, 16)
To graph f(x)
- Plot the vertex
- Plot the x-intercepts
- Plot the y-intercept
- Draw a parabola opening downwards with the vertex as the maximum point.
The axis of symmetry is the x-value of the vertex. Use this to help ensure the curve is symmetrical.