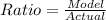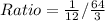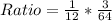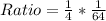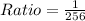Question

An architect makes a model of a new house. The model shows a tile patio in the backyard. In the​ model, each tile has length

one half in.12 in.
and width
one sixth in.16 in.
The actual tiles have length
two thirds ft23 ft
and width
two ninths ft29 ft.
What is the ratio of the length of a tile in the model to the length of an actual​ tile? What is the ratio of the area of a tile in the model to the area of an actual​ tile? Use pencil and paper. Describe two ways to find each ratio.


The ratio of the length of a tile in the model to the length of an actual tile is

Answer 1

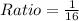`Ratio = (1)/(16)` ----- Model length to Actual length

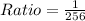`Ratio = (1)/(256)` ----- Model Area to Actual Area

Step-by-step explanation:

Given

Model Measurement:

`Length = (1)/(2)\ in`

`Width = (1)/(6)\ in`

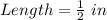
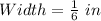
Actual Measurement:

`Length = (2)/(3)\ ft`

`Width = (2)/(9)\ ft`

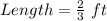
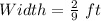
Solving (a): Ratio of actual length to model length

Convert length from feet to inches

`Length = (2)/(3)\ ft`

`Length = (2)/(3)\ * 12in`

`Length = (24\ in)/(3)`

`Length = 8\ in`

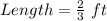
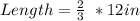
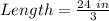
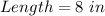
The required ratio is calculated by dividing the model length by the actual length

`Ratio = (Model)/(Actual)`

`Ratio = (1)/(2)\ in/8\ in`

`Ratio = (1)/(2)/8`

`Ratio = (1)/(2) * (1)/(8)`

`Ratio = (1)/(16)`

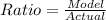
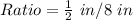
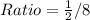
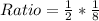
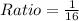
Another possible way is to convert both measurement to a different unit:

Convert model length from inches to cm

`Length = (1)/(2)\ in`

`Model\ Length = (1)/(2) * 2.54cm`

`Model\ Length = (1 * 2.54cm)/(2)`

`Model\ Length = (2.54cm)/(2)`

`Model\ Length = 1.27 cm`

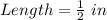
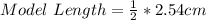
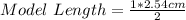
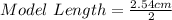
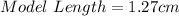
Convert actual length from ft to cm

`Length = (2)/(3)\ ft`

`Actual\ Length = (2)/(3) * 30.48cm`

`Actual\ Length = (2 * 30.48cm)/(3)`

`Actual\ Length = (60.96cm)/(3)`

`Actual\ Length = 20.32cm`

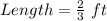
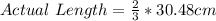
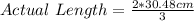
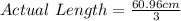
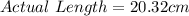
Then calculate the ratio as:

`Ratio = (Model)/(Actual)`

`Ratio = (1.27cm)/(20.32cm)`

`Ratio = (1.27)/(20.32)`

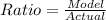
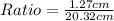
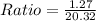
Simplify fraction

`Ratio = (1.27/1.27)/(20.32/1.27)`

`Ratio = (1)/(16)`

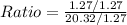
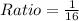
Solving (b): Model of Area;

Way 1:

In (a), we calculated the ratio of length to be:

`Ratio = (1)/(16)`

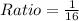
This is also the model of the width.

So, Ratio of Area is then calculated as:

`Ratio = (1)/(16)^2`

`Ratio = (1)/(256)`

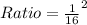
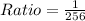
Way (2): We calculate the actual area of the model and actual measurements.

Model Measurements

`Length = (1)/(2)\ in`

`Width = (1)/(6)\ in`

`Area = Length * Width`

`Area = (1)/(2) * (1)/(6) in^2`

`Area = (1)/(12)\ in^2`

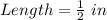
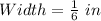
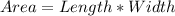
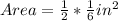
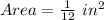
Actual Measurements

`Length = (2)/(3)\ ft`

`Width = (2)/(9)\ ft`

`Area = Length * Width`

`Area = (2)/(3) * (2)/(9) ft^2`

`Area = (4)/(27) ft^2`

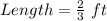
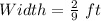
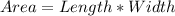
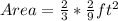
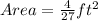
Convert to
`in^2`

`Area = (4)/(27) * 144in^2`

`Area = (4)/(3) * 16in^2`

`Area = (64)/(3)in^2`

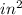
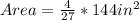
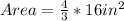
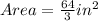
Ratio is then calculated as:

`Ratio = (Model)/(Actual)`

`Ratio = (1)/(12)/(64)/(3)`

`Ratio = (1)/(12) * (3)/(64)`

`Ratio = (1)/(4) * (1)/(64)`

`Ratio = (1)/(256)`