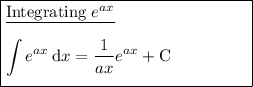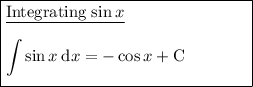Answer:

Step-by-step explanation:
Given differential equation and initial condition:
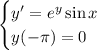
Rearrange the differential equation so that all the terms containing y are on the left-hand side, and all the terms containing x are on the right-hand side:
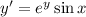
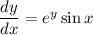


Integrate both sides of the equation:

Substitute the given condition y(-π) = 0 into the equation and solve for C:

Substitute the found value of C into the equation:

Multiply both sides by -1:
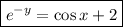

Integration rules used: