Question

Do you remember learning about the discriminant? For a quadratic equation of the form:

ar²+bx+c
The discriminant is equal to:
6² - 4ac
It tells us how many solutions a quadratic equation has. The discriminant can give us three results regarding the roots of an equation.
a) What are these three different results? What are the discriminants for each and what would the graph look like?
b) Where does the discriminant come from?

Answer 1

Explanation:

Discriminant:

`\sf Quadratic \ formula = (-b \± \ √(b^2-4ac))/(2a)`

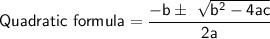
Discriminant is the part of the quadratic formula inside the square root. It determines whether the quadratic equation has real roots or not.

Discriminant = b² - 4ac

Here b is the coefficient of x ; a is the coefficient of x² and c is the constant.

• If b² - 4ac > 0 then the quadratic equation has two distinct real roots.
• If b² - 4ac = 0, then the quadratic equation has two equal real roots.
• If b² - 4ac <0, then the quadratic equation has no real roots.