Answer: a.) $50188 to $57812
Explanation: Confidence Interval (CI) is an interval of values in which we are confident the true mean is in.
The interval is calculated as
x ±
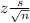
a. For a 95% CI, z-value is 1.96.
Solving:
54,000 ±
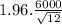
54,000 ±
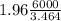
54,000 ± 1.96*1732.102
54,000 ± 3395
This means the interval is
50605 < μ < 57395
With a 95% confidence interval, the mean starting salary of college graduates is between 50605 and 57395 or from 50188 to 57812$.
b. The mean starting salary for college students in 2017 is $50,516, which is in the confidence interval. Therefore, since we 95% sure the real mean is between 50188 and 57812, there was no significant change since 2017.